Ecuaciones de la Recta
Ecuación vectorial de la recta
Ecuaciones paramétricas de la recta
Si operamos en la ecuación vectorial de la recta llegamos a la igualdad:

Para que se verifique esta igualdad, se deben cumplir:

Ecuaciones continuas de la recta
Despejando e igualando λ en las ecuaciones paramétricas se tiene:

Ecuaciones implícitas de la recta
Una recta puede venir determinada por la intersección de los planos.

Si en las ecuaciones continuas de la recta quitamos denominadores y pasamos todo al primer miembro, obtenemos también las ecuaciones implícitas.
Haz de Planos

Llamamos haz de planos de arista una recta r dada, al conjunto de los planos que contienen a dicha recta r. Es decir, es la recta donde cortan los planos como podemos ver en la siguiente imagen.
Supongamos que una recta viene dada por su ecuación implícita:
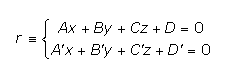
Hemos visto que para un plano π: A”x+B”y+C”z+D”=0 contenga a la recta r debe cumplirse que el rango de la matriz formada por las filas (A,B,C), (A’,B’,C’) (A”,B”,C”) tiene que coincidir con el rango de la matriz ampliada, formada por las filas (A,B,C,D), (A’,B’C’,D’) y la fila (A”,B”,C”,D”), este rango es 2. Por tanto, (A”,B”,C”,D”) es combinación lineal de los otros dos vectores. De esta manera obtenemos el haz de planos de arista la recta r: (Ax+By+Cz+D)+λ(A’x+B’y+C’z+D’)=0, con λ una constante real no nula.
Supongamos que una recta viene dada por su ecuación implícita:
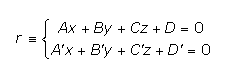
Hemos visto que para un plano π: A”x+B”y+C”z+D”=0 contenga a la recta r debe cumplirse que el rango de la matriz formada por las filas (A,B,C), (A’,B’,C’) (A”,B”,C”) tiene que coincidir con el rango de la matriz ampliada, formada por las filas (A,B,C,D), (A’,B’C’,D’) y la fila (A”,B”,C”,D”), este rango es 2. Por tanto, (A”,B”,C”,D”) es combinación lineal de los otros dos vectores. De esta manera obtenemos el haz de planos de arista la recta r: (Ax+By+Cz+D)+λ(A’x+B’y+C’z+D’)=0, con λ una constante real no nula.
Ejemplo: a) Halla la ecuación del haz de planos que contiene a la recta
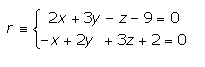
b) Hallar la ecuación del plano correspondiente al haz anterior que pasa por el punto P(3,2,-3).
a) La ecuación del haz es: (2x+3y-z-9)+ λ(-x+2y+3z+2)=0.
b) Sustituyendo el punto en la ecuación del haz el punto, obtenemos que λ=1. Sustituyendo este valor en la ecuación del haz obtenemos el plano pedido: π: 2x+3y-z-9-x+2y+3z+2=0 → π: x+5y+2z-7=0.
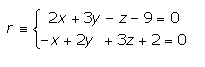
b) Hallar la ecuación del plano correspondiente al haz anterior que pasa por el punto P(3,2,-3).
a) La ecuación del haz es: (2x+3y-z-9)+ λ(-x+2y+3z+2)=0.
b) Sustituyendo el punto en la ecuación del haz el punto, obtenemos que λ=1. Sustituyendo este valor en la ecuación del haz obtenemos el plano pedido: π: 2x+3y-z-9-x+2y+3z+2=0 → π: x+5y+2z-7=0.

 .
.



No hay comentarios:
Publicar un comentario