Clase #3

El Plano en el Espacio

Siendo que el vector n es perpendicular al plano, al hacer producto punto de n con el vector PM obtenemos:

Ecuación vectorial plano

$$(\overrightarrow { r } -\overrightarrow { ro } )\cdot \quad \overrightarrow { n } =\quad 0$$

de la cual se obtiene la Ecuación General:

$$Ax\quad +\quad By\quad +\quad Cz\quad +\quad D\quad =0$$

Ecuaciones incompletas:

1) Si C=0 -> Ax + By + D = 0

Ecuación del plano con generatriz paralela al eje OZ.

2) Si C=0 y D=0 -> Ax + By 0

Ecuación del plano con generatriz paralela al eje OZ. Plano contiene al eje OZ.

3) Si B=0 y C=0 y D ≠ 0 -> Ax + D = 0

Ecuación del plano con generatrices paralelas al eje OZ y OY.

*Lo mismo sucede para los demás casos con A=0.

4) Si B=D=C=0 -> Ax  = 0

x=0 y se encuentra en el Plano YOZ

*Lo mismo sucede para los demás casos con B ≠ 0 y C ≠ 0.

Adicionalmente tenemos:

Ecuación segmentaria del plano


A partir de la Ecuación General, podemos dividir todo para D y obtener:

$$\frac { X }{ -\frac { D }{ A }  } +\frac { Y }{ -\frac { D }{ B }  } +\frac { Z }{ -\frac { D }{ C }  } =\quad 1$$


Ecuación normal del plano
Siendo el vector unitario n:
$$\hat { n } =\quad (\cos { \alpha \quad , } \cos { \beta \quad , } \cos { \gamma  } )$$
y rho:
$$\rho \quad =\quad \hat { A } \cdot \overrightarrow { B } $$
La Ecuación normal del plano es:
$$x\cos { \alpha \quad + } y\cos { \beta \quad + } z\cos { \gamma  } -\quad \rho \quad =\quad 0$$

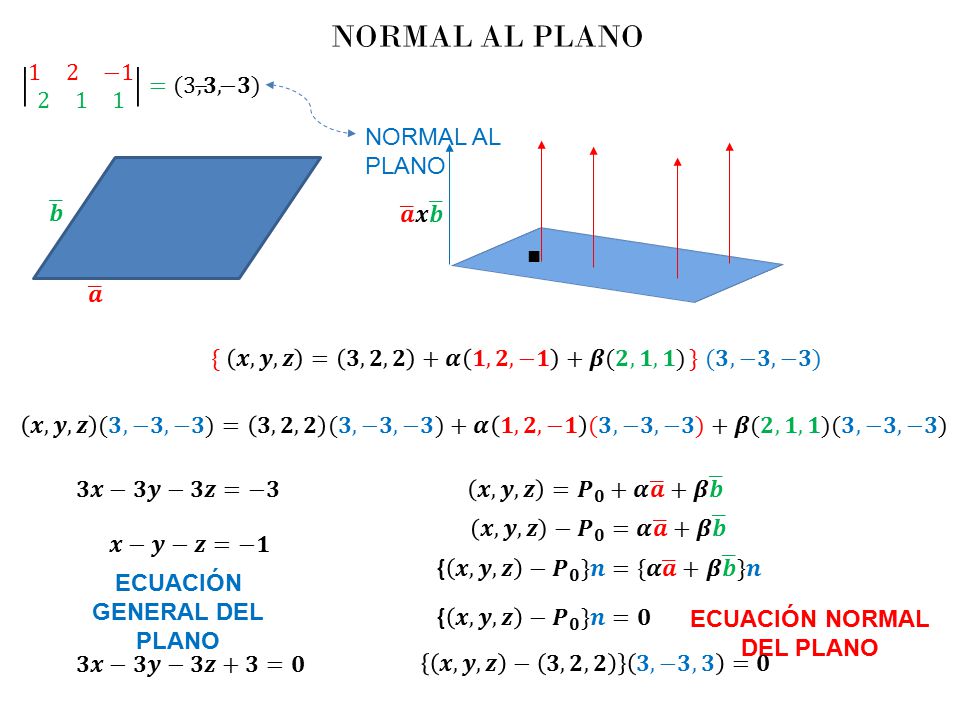
Ejemplo: