Clase #4

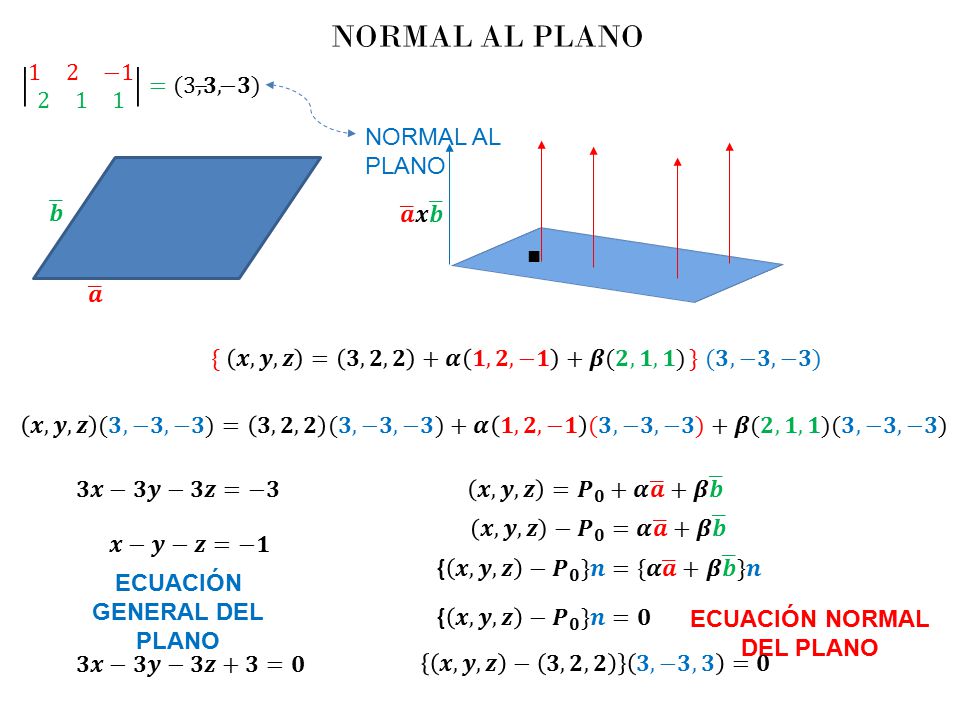
Normalización de la ecuación general del plano.

Siendo que:

Ax + By + Cz + D = 0

$$x\cos { \alpha \quad  } + y\cos { \beta \quad } +  z\cos { \gamma }  -\quad \rho \quad =\quad 0$$

u lo multiplicamos por la ecuación general y va a ser nuestro factor normalizante.

Obtenemos la siguiente fórmula:

$$u\quad =\quad \pm \frac { 1 }{ \sqrt { { A }^{ 2 }+B^{ 2 }+C^{ 2 } }  } $$

Donde el signo del factor normalizante debe ser opuesto al signo de D en la ecuación.

Desviación de un punto respecto de un plano

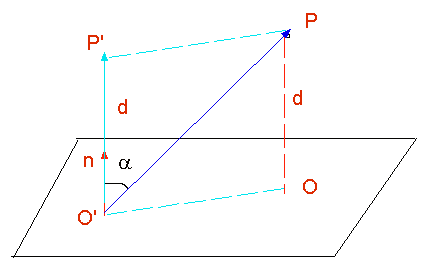
- d es positiva cuando el punto P y el origen de coordenadas están en lados opuestos al plano.

- d es negativa cuando el punto P debajo del plano y el origen de coordenadas están en el mismo lado del plano.

Distancia de un punto al plano

$$d\quad =\quad \frac { x1A\quad +\quad y1B\quad +\quad z1C\quad +D }{ \sqrt { { A }^{ 2 }+B^{ 2 }+C^{ 2 } }  } $$

Ecuación de un plano dado 3 puntos

$$(\overrightarrow { r } -\overrightarrow { r1 } )\quad \bullet \quad ((\overrightarrow { r2 } -\overrightarrow { r1 } )\quad x\quad (\overrightarrow { r3 } -\overrightarrow { r1 } ))\quad =\quad 0$$

Observación:

Si el producto mixto es igual a cero, entonces los 3 vectores involucrados son coplanares.

El producto misxto, geométricamente representa el volumen del paralelepípedo cuyas aristas son los 3 vectores involucrados.

Volumen de un paralelepípedo

El volumen en general es el área de la base por la altura, siendo el volumen de la base el módulo del producto cruz de los vectores que definen los lados de la base.

$$h\quad =\quad \left| \overrightarrow { C }  \right| \bullet \quad \sin { \alpha  } $$

$$ V\quad =\quad \overrightarrow { A } x\overrightarrow { B } \bullet \overrightarrow { C } $$

Clase #3

El Plano en el Espacio

Siendo que el vector n es perpendicular al plano, al hacer producto punto de n con el vector PM obtenemos:

Ecuación vectorial plano

$$(\overrightarrow { r } -\overrightarrow { ro } )\cdot \quad \overrightarrow { n } =\quad 0$$

de la cual se obtiene la Ecuación General:

$$Ax\quad +\quad By\quad +\quad Cz\quad +\quad D\quad =0$$

Ecuaciones incompletas:

1) Si C=0 -> Ax + By + D = 0

Ecuación del plano con generatriz paralela al eje OZ.

2) Si C=0 y D=0 -> Ax + By 0

Ecuación del plano con generatriz paralela al eje OZ. Plano contiene al eje OZ.

3) Si B=0 y C=0 y D ≠ 0 -> Ax + D = 0

Ecuación del plano con generatrices paralelas al eje OZ y OY.

*Lo mismo sucede para los demás casos con A=0.

4) Si B=D=C=0 -> Ax  = 0

x=0 y se encuentra en el Plano YOZ

*Lo mismo sucede para los demás casos con B ≠ 0 y C ≠ 0.

Adicionalmente tenemos:

Ecuación segmentaria del plano


A partir de la Ecuación General, podemos dividir todo para D y obtener:

$$\frac { X }{ -\frac { D }{ A }  } +\frac { Y }{ -\frac { D }{ B }  } +\frac { Z }{ -\frac { D }{ C }  } =\quad 1$$


Ecuación normal del plano
Siendo el vector unitario n:
$$\hat { n } =\quad (\cos { \alpha \quad , } \cos { \beta \quad , } \cos { \gamma  } )$$
y rho:
$$\rho \quad =\quad \hat { A } \cdot \overrightarrow { B } $$
La Ecuación normal del plano es:
$$x\cos { \alpha \quad + } y\cos { \beta \quad + } z\cos { \gamma  } -\quad \rho \quad =\quad 0$$

Ejemplo:

Clase #2

Sistema de funciones implícitas.

F(x,y)=0

G(x,y)=0 

*Cada una de las funciones implícitas representa una curva, por tanto la solución del sistema será uno o más puntos.



En R^3 F(x,y,z)=0 que es una función implícita de 3 variables.
Hay casos especiales como F(x,y)=0 que es una superficie en R^3 con generatriz paralelo al eje OZ, como también sucede el caso especial que pueden ser paralelas a los demás ejes.


Si F(x,y,z) =0
Representa una superficie cuya generatriz no es paralela a ningún eje coordenado.

Sistema de Funciones Implícitas
F(x,y,z) =0
G(x,y,z) =0

En un sistema de funciones ímplicitas en R3 si se tienen 2 funciones implícitas generalmente representan curvas en el espacio vectorial R3, mientras que si se tiene 3 funciones implícitas la solución son puntos.

En general Ax +By +Cz + D =0 es una función implícita de primer grado y representa un plano cuya generatriz no es paralela a ningún eje.

La recta


Dados 2 puntos se puede calcular la ecuación de la recta en el espacio.
Siendo:
a)Ecuación vectorial:
$$\overrightarrow { OX } =\quad t*\overrightarrow { u } +\overrightarrow { OP } ; \overrightarrow { u } = (l,m,n) $$
b) Ecuación Paramétrica:
X = Xo + t*l
Y =Yo + t*m
Z = Zo + t*n
c) Ecuación caretsiana:
$$\frac { X\quad -Xo }{ l } =\frac { Y\quad -Yo }{ m } =\frac { Z\quad -Zo }{ n } $$

    

Clase #1

Indicaciones Generales

Las actividades y tareas están detalladas en la sección correspondiente

Para la realización de las tareas se deben tener las siguientes indicaciones:

Papel boon tamaño A4

Margen en todas las hojas usadas

Encabezado en la primera hoja que debe contener:

Escuela Politécnica Nacional
Carrera
Materia
Nombre
Fecha
Tema

Presentar en la fecha señalada, se valorará la responsabilidad y cumplimiento

Una vez registrada la tarea y devuelta con la firma, escanear y subir al Portafolio estudiantil en la sección EVIDENCIAS.

Portafolio estudiantil

El  Portafolio estudiantil debe contener:
Contexto-¿Quienes somos?-¿Donde estamos?-¿Qué?-¿Para qué?
Nombre completo del estudiante y fotografía
Un breve resumen de temas revisados en clases para cada semana.

ABRIL

Contexto-¿Quienes somos?-¿Donde estamos?-¿Qué?-¿Para qué?Nombre completo del estudiante y fotografíaUn breve resumen de temas revisados en clases para cada semana.

ABRIL

MAYO

JUNIO

JULIO

EVIDENCIAS: Los enlaces a los documentos creados en Google-Drive con las imágenes de las tareas ya firmadas.

Geometría Analítica 

AxB ={ (x,y) pertenece a R^2 / x pertenece a A ^ y pertenece a B }
BxA ={ (x,y) pertenece a R^2 / x pertenece a B ^ y pertenece a A }

En R^2 F (x,y) =0
1. Si y = f (x) v y = f2 (x)
2. Si x = g (y) v y = g2 (y)

La recta es la curva más simple.
Generalmente la recta de una función implícita representa una curva en el plano.

x^2 +y^2 <=9 es un círculo
x^2 +y^2 =9 es una circunferencia.